人工智能教程 数学基础课程1.1 数学分析v2 实数的连续性和完备性

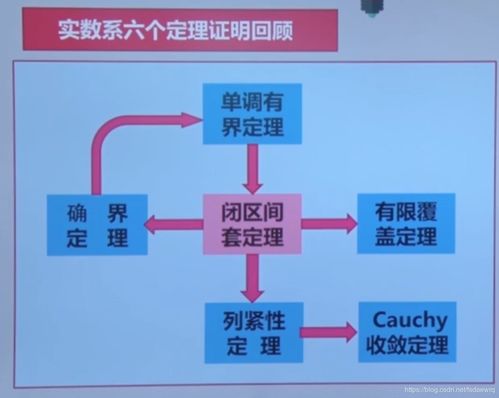
在人工智能的基础软件开发中，数学分析扮演着至关重要的角色。本课程是数学基础课程的第一部分，聚焦于实数的连续性和完备性，这两个概念为理解数据处理的连续性、优化算法的收敛性以及机器学习模型的稳定性奠定了理论基础。

一、实数的连续性

实数的连续性是指实数轴上的点没有“间隙”，任何两个不同的实数之间都存在无限多个其他实数。这一性质源于实数的基本性质，例如，任意有上界的非空实数集必有上确界。连续性在人工智能中至关重要，因为它确保了函数的连续性分析，这在梯度下降等优化算法中被广泛应用。例如，在训练神经网络时，我们经常处理连续损失函数，其导数依赖于实数的连续性以找到最小值点。

二、实数的完备性

实数的完备性意味着实数集是“完整”的，即任何柯西序列（一种逐渐趋近的序列）在实数集中都有极限点。这一定义源于实数系统的构造，例如戴德金分割或康托尔公理。在人工智能基础软件开发中，完备性保证了算法的收敛性。例如，在机器学习中，许多迭代算法（如随机梯度下降）依赖于实数空间的完备性来确保模型参数最终收敛到最优解，避免了因数值不完整导致的发散问题。

三、实际应用与总结

实数的连续性和完备性共同支撑了人工智能软件的开发。在数据处理中，连续性允许我们对传感器数据进行平滑处理；在算法设计中，完备性确保优化过程稳定。理解这些概念有助于开发者设计更高效的AI系统，避免数值错误。本课程旨在强化数学基础，为后续深入学习人工智能算法打下坚实基础。继续学习下一节，我们将探讨函数的极限与连续性。